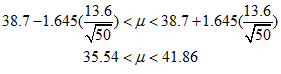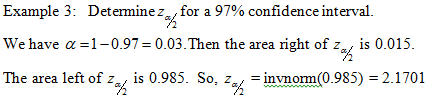
Confidence Intervals for Population Means When σ is Known
What it means: Suppose you are told that the 90% confidence interval for the mean is 28.7 < m < 36.7. This means that from data gathered there is a 90% chance that the
population mean is between 28.7 and 36.7.
The Idea: Gather a sample of size n from a population with known standard deviation σ and use its mean X to construct a confidence interval for m.
Note: We call X a point estimate of m. If all you know is X then it is the best estimate you have of the population mean.
What we need to construct a 95% confidence interval:
Problem: Find the z-scores in the standard normal distribution for the ends of the interval that contains the middle 95% of values.
We use the Greek letter alpha, a, for 1 - 0.95 = 0.05. (If we want the middle 90% of values then a = 1 - 0.9 = 0.1 and so on.)
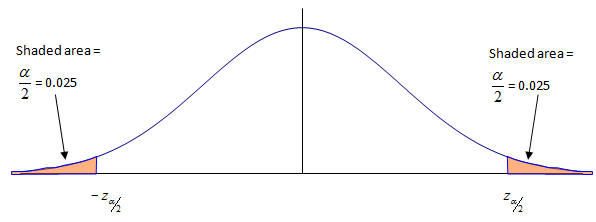
If we put an area a/2 = 0.025 in each tail then the area of the region between the shaded regions will be 0.95 and hence the probability that a randomly selected
z will lie in the unshaded region is 0.95
Then we have the following picture:

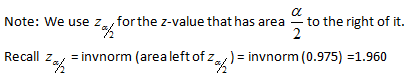
Recall that if the area right of z is .025, then the area left of z is 1 - 0.025 = 0.975
The formula for a confidence interval:
Example 1: A population is known to have standard deviation 13.6. You take a sample of size 50 and find its mean is 38.7. Construct a 95% confidence interval for the population mean.
Example 1: A population is known to have standard deviation 13.6. You take a sample of size 50 and find its mean is 38.7. Construct a 95% confidence interval for the population mean.
The interval is:
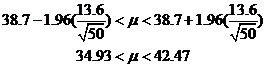
Example 2: Construct a 90% confidence interval for the data in Example 1.
What we need to construct a 90% confidence interval.