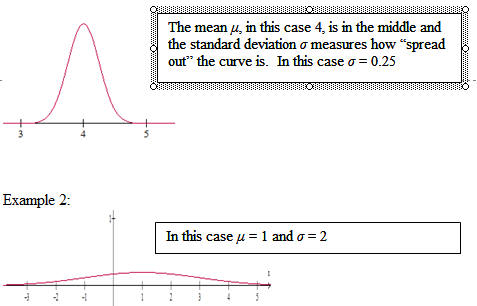
Normal Distributions

A normal distribution is represented by a symmetric bell-shaped curve.  The curves extend for ever in both directions.  As you can see from the graphs a fair distance from the middle there is essentially nothing you can measure.  In all cases the total area under the curve is 1.

Example 1:

Note: We use X to represent a value in a normal distribution.  In a normal distribution the probability that X is equal to a particular value is 0.  In symbols

P(X = k) = 0.  We consider probabilities that X lies in a range of values.  The probabilities are equal to areas under the curve.

The probability that X lies between a and b, in symbols P(a < X < b) is the shaded area.

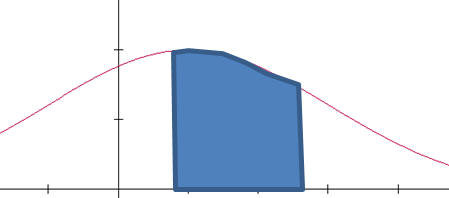
                                          a                              b

The probability that X is less than a, in symbols P( X < a) is the shaded area:

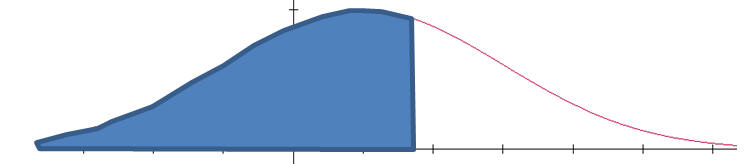
                                                           a

The probability that X is greater than a, in symbols P( X > a) is the shaded area:

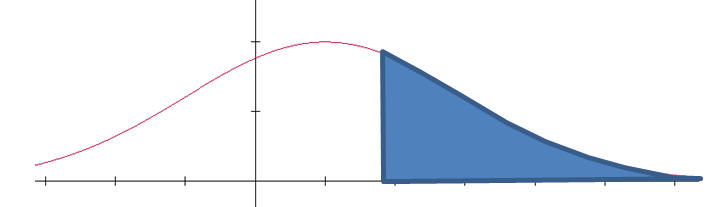
                                                                                              a

In order to calculate probabilities we use the standard normal distribution, which has mean = 0 and standard deviation = 1.  We use z for the variable, which

represents z-score as introduced earlier:

This is a graph of the standard normal distribution.  You do not need to know it, but the function is  

Example 3:  A normal distribution has mean 10 and standard deviation 2.  Fine the probability that a randomly selected value lies between 7 and 11.  That is,

P(7 < X < 11) .  You convert 7 and 11 to z-scores

Then P(7 < X < 11) = P( ̶  1.5 < z < 0.5)

On a TI83+ this is calculated as normalcdf ( ̶ 1.5, 0.5) = 0.6247.

Example 4:  A normal distribution has mean 10 and standard deviation 2.  Fine the probability that a randomly selected value is less than 6.  That is,

P( X < 6) .  You convert 6 to a z-score

Then P(X < 6) = P (z <  ̶  2)

On a TI83+ this is calculated as normalcdf ( ̶ 10000, ̶ 2) = 0.0228.  (you can use any large negative number in place of  ̶ 10000)

Example 5:  A normal distribution has mean 10 and standard deviation 2.  Fine the probability that a randomly selected value is greater than 11.5.  That is,

P( X >11.5) .  You convert 11.5 to a z-score

Then P(X > 11.5) = P (z > 0.75)

On a TI83+ this is calculated as normalcdf ( 0.75, 10000) = 0.2266.  (you can use any large positive number in place of 10000)