Finding Values in Normal Distributions

Example 1:  Find X such that 47% of values in a normal distribution with mean 23.2 and standard deviation 5.8 are less than X.

In this type of problem you fist find the z-score for X and then convert to X using X = m + sz.

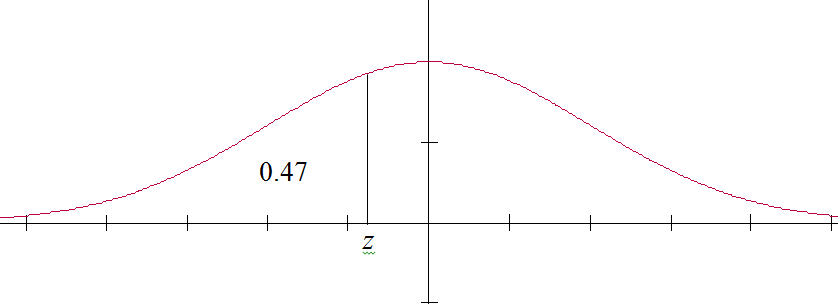
The picture for z in the standard normal distribution is

Note that the area to the left of z is 0.47.  Note that the total area under the curve is 1, so the area left of center is 0.5, making z somewhat to the left of center.  On the TI83+ to find z use invNorm(area left of z).  In this case z = invNorm(0.47) =  ̶  0.0753

Then  X = m + sz = 23.2 + ( ̶  0.0753)5.8 = 22.7 (The answer is rounded to one decimal place because the given values have one decimal place.)

Example 2:  A admissions test has a mean of 237 and a standard deviation of 36.  Only the top 10% will be selected for admission.  Find the cut-off admission score.  Round to the nearest whole number.

The z-score for the cut-off is found using the following picture:

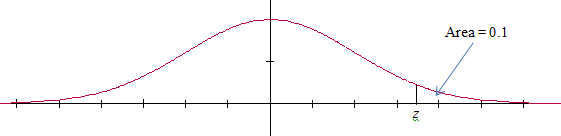
To find z on a TI83+ you need the area to the left of z.  Since the total area is 1 the area left of z is 1 ̶  0.1 = 0.9.  Then z = invNorm(0.9) = 1.282.

Then X = m + sz = 237 + 36(ans) = 283.14.  The cut-off score is 283

Example 3:  A admissions test has a mean of 237 and a standard deviation of 36.  Find the range for the middle 50% of scores.  Round answers to the nearest whole number.

You need to find z-scores that cover the middle 50% of values.  Since the picture is symmetric you get values z and  ̶  z  as in the following picture:

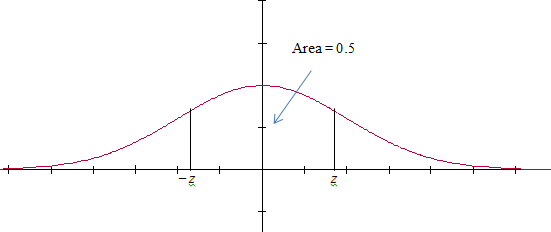
To find z on a TI83+ you need the area to the left of z.  Since the total area is 1 the area in the tails is 1 ̶  0.5 = 0.5 .  The picture is symmetice so half of 0.5, or 2.5 must be in each tail making the total area left of z = 0.75. Then z = invNorm(0.75) = 0.6745.

The scores that cover the middle 50 of values are  X = m + sz = 237 + 36(0.6745) = 261.282 and X = m  ̶  sz = 237 ̶ 36(0.6745) =212.78  The range for the middle 50% of scores is 213 to 261.