Testing if Two Means are Different
Note: This is a brief summary of part of Section 11.2. There is much more information in the section which you are invited to read.
The problem: You have two samples
from independent populations, that is, thee data in one sample does not affect data
in the other sample. The sample means are
![]() and
and
![]() the
sample standard deviations are s1 and s2 and the sample
sizes are n1 and n2. You want to test if the population
means m1 and
m2 are different.
the
sample standard deviations are s1 and s2 and the sample
sizes are n1 and n2. You want to test if the population
means m1 and
m2 are different.
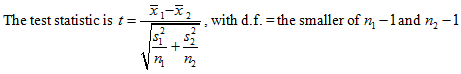
Note: When setting up these tests
start with the alternative hypothesis, which is what you are trying to show to
be true or false. In a two tailed test it is
![]() . (Alternatively
m1 -
m2 ≠
0)
For a left-tailed test it is
. (Alternatively
m1 -
m2 ≠
0)
For a left-tailed test it is ![]() (Alternatively
m1 -
m2 < 0) and
for a right-tailed test it is
(Alternatively
m1 -
m2 < 0) and
for a right-tailed test it is ![]() (Alternatively
m1 -
m2 > 0)
(At least in any example I give you)
(Alternatively
m1 -
m2 > 0)
(At least in any example I give you)
A Two-Tailed Test
Gardener Joe wants to try a new, and cheaper, fertilizer on his broad beans. He fertilizes 30 plants with the old fertilizer and finds that the mean yield is 31 ounces with a standard deviation of 5 ounces. He fertilizes 15 plants with the new fertilizer and finds the mean yield is 29 ounces with a standard deviation of 6 ounces. Can he conclude that the mean yields are different. Use a = 0.05.
The data can be summarized as follows. It does not matter which data set uses the subscript 1.

How to set it up: H0: m1 = m2 Alternatively H0: m1 - m2 = 0
H1: m1 ≠ m2 H1: m1 - m2 ≠ 0
Reject H0 if P < 0.05
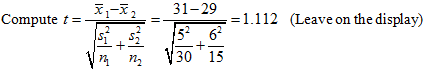
Since t is in the right tail compute the area right of t and double it because the test is two tailed
P = 2tcdf(ans, 10000, 14) = 0.2848 Note: d.f. = 15- 1
Do not reject H0 because P > a. The new fertilizer does not make a difference.
A Right-Tailed Test

Change the assumption population standard deviation is the sample standard deviation
The data can be summarized as follows
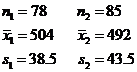
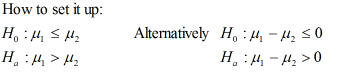
Reject H0 if P < 0.01
Compute
 =1.868
=1.868
Compute P = tcdf(ans, 10000, 77) = 0.328
Because P is larger than the level of significance do not reject the null hypothesis. The prep course does not improve the scores.
Note: Whenever you are wanting
to show ![]() the
test is right tailed. You will always get a positive value for t and you
compute the area right of t to find P.
the
test is right tailed. You will always get a positive value for t and you
compute the area right of t to find P.
A Left-Tailed Test

Change the assumption to assume the population variances are unequal
The data can be summarized as follows
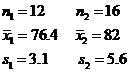
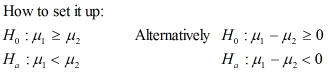
Reject H0 if P < 0.05
Compute

Compute P = tcdf( −10000, ans,11) = 0.0035
Because P is smaller than the level of significance reject the null hypothesis. Students in traditional lab courses scored lower
Note: Whenever you want to show
![]() the
test is left tailed. You will always get a negative value for t and you
compute the area left of t to find P.
the
test is left tailed. You will always get a negative value for t and you
compute the area left of t to find P.