
What is Probability?
Probability measures how likely some event is to occur. It is a number between 0 and 1 based on how frequently you expect the
event to occur. For example if you toss a fair coin, fair meaning heads and tails are equally likely, the you expect to get heads half of the time, so the
probability of getting heads is 0.5
To be technically correct a probability is a number between 0 and 1. However you often see probabilities given as percentages. If you want to use a percent, call it a chance: The chance of getting heads is 50%.
Subjective Probability
Subjective probability is based on what you will believe will happen. For example: The probability I will take a vacation next year is 0.75
Empirical Probability
Empirical probability measures how likely an event is to occur based on past events.
Example 1: When the weather forecast is for a 60% chance of rain it means that in the past in similar conditions it has rained 60% of the time. This means that the probability of rain is 0.6.
Example 2: If 60 out of the last 100 cars to drive by have been Fords. The empirical probability that the next car is a ford is 0.6
Classical probability
In classical probability you have a sample space consisting of predetermined equally likely outcomes. You conduct experiments.
Example 1: The experiment is rolling a fair six sided die. The sample space consists of the six outcomes 1, 2, 3, 4, 5, 6
Example 2: The experiment is to toss a fair coin. The sample space consists of two outcomes H, T
Example 3: The experiment is to draw a card from a standard 52 card deck. The sample space is below

Source: “Elementary Statistics” by Allan G. Bluman.
Example 4. The experiment is to roll two dice. The sample space is below
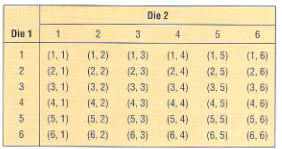
Source: “Elementary Statistics” by Allan G. Bluman.
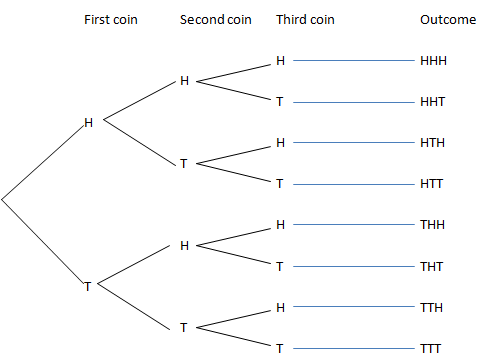
Tree Diagrams
A tree diagram can be used to help determine a sample space. Suppose the experiment is to toss three coins.
You can get H or T on the first coin, then each of these can be followed by H or T on the second coin, giving four outcomes for the first two coins. Then each of these four outcomes can be followed by H or T giving eight outcomes in total
Events
An event E consists of a set of outcomes in a probability experiment.
Example 1: The experiment is to draw a card from a standard 52 card deck and the event E consists of the clubs in the deck. You say that E occurs if you draw a club
Example 2: The experiment is to roll two dice. The event E is for the sum of the faces to be 7
We we use P(E) for the probability that the event E occurs. To make things easier to read we often write a description of the event in place of E. For example when drawing a card P(Draw a club)
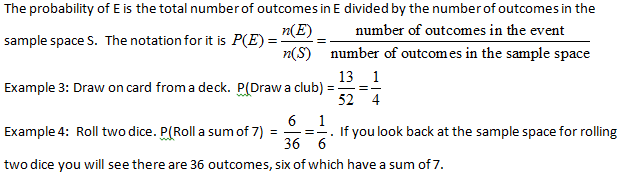
AND Type Events
If you have two events A and B, then the event A and B is the event that both A and B occur.
Example 1: The experiment is to roll a die. The events are A: roll an even number and B: roll greater than 3.
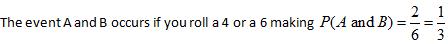
Example 2: Toss three coins. What is the probability of getting two tails?

Example 3: Draw a card from a 52 card deck. The events are A: draw a diamond and B: draw a spade.
It is impossible for one card to be both a diamond and a spade so A and B cannot occur. When an event cannot occur its probability is zero. So, P(A and B) = 0.
OR Type Events
If you have two events A and B, then the event A or B is the event that A occurs, B occurs or both A and B occur.
Example 1: The experiment is to roll a die. The events are A: roll an even number and B: roll greater than 2.
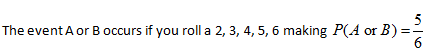
Example 2: Draw a card from a 52 card deck. The events are A: draw a red card and B: draw a black card.
Now it is certain that A or B occurs because it contains all 52 outcomes. When an event is certain its probability is 1. So, P(A or B) = 1
Complementary Events
If E is and event then its complement E is the event that E does not occur. For example if you roll a die and E is the event that you roll an odd number, then E is the event that you roll an even number.
The following are always true:
P(E) = 1 ̶ P(E) P(E) = 1 ̶ P(E) P(E) + P(E)= 1
There will be some problems where it is easier to work with the complement. For now consider the following example:
Forty seven percent of a secret society's members are women. If you select one member at random what is the probability that you will select a man?
Since 47% are women the probability you will select a woman is 0.47. The complementary event is to select a man, so the probability of selecting a man is 1 ̶ 0.47 = 0.53
Addition Rules
Events A and B are mutually exclusive if they cannot occur together.
For mutually exclusive events P(A or B) = P(A) + P(B) Explanation
The probability that you get two heads when you toss three coins is 0.375; The probability you get three heads is 0.125.
It is not possible to get two head and three heads at the same time so the events are mutually exclusive.
So the probability you get two or thee heads is 0.375 + 0.125 = 0.5
Events A and B are not mutually exclusive if they can occur together.
For events that are not mutually exclusive P(A or B) = P(A) + P(B) ̶ P(A and B) Explanation
Example 1: Draw one card from a deck. What is the probability that you draw red card and an ace?
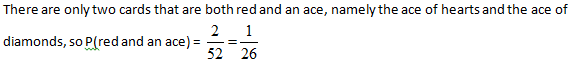
Example 2: Draw one card from a deck. What is the probability that you draw red card or an ace?
There are 26 red cards and 4 aces so,
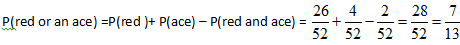
Example3: The following represents the number of college degrees awarded in one year
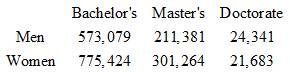
One student is selected at random.
Find
(a) The probability the student received a bachelor’s degree
(b) What is the probability the student was a woman or received a doctorate?
(c) What is the probability the student was a woman who received a doctorate?

Note: In classical probability where you have exact answers you give exact answers using fractions.
The above figures are likely not 100% accurate, because the numbers constantly change. In such situations it is standard to answer with a rounded decimal.
We will answer part c next because it is used in part b
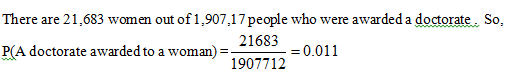
b. P(A doctorate or a degree awarded to a woman) = P(doctorate) + P(awarded to a woman) ̶ P(A doctorate awarded to a woman) =
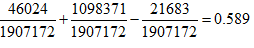
d. Use a complement.
