Quartiles
Quartiles divide data into four sets of equal size, or at least as close as you can get to four sets of equal size.
The first quartile, Q1, is the 25th percentile
The second quartile, Q2, is the 50th percentile, which is also the median
The third quartile, Q3, is the 75th percentile
The quick way to find the quartiles is to first put the data in order. For example data is 3, 1, 6, 7, 4, 2, 12, 31, 22, 19, 16.
In order the data is 1, 2, 3, 4, 6, 7, 12, 16, 19, 22, 31
First find Q2, which is the median: Q2 = 7
You then look at the data left of where the median is 1, 2, 3, 4, 6.
Then Q1 is the median of these values: Q1= 3.
Finally look at the data to the right of where the median is: 12, 16, 19, 22, 31
Then Q3 is the median of these values: Q3= 19.
Note that highlighting the quartiles is red shows that you are as close as you can be to four sets of equal size
1, 2, 3, 4, 6, 7, 12, 16, 19, 22, 31
Now suppose you add a value to get data 1, 2, 3, 4, 6, 7, 12, 16, 19, 22, 31, 64
First find Q2, which is the median: Q2 = (7+12)/2 = 9.5
Now the position of the median is between the sixth anf seventh values, so data to the left of the position of the median is
1, 2, 3, 4, 6, 7
Then Q1 is the median of these values: Q1= 3.5.
Finally look at the data to the right of where the median is: 12, 16, 19, 22, 31, 64
Then Q3 is the median of these values: Q3= 20.5.
The Five Number Summary
The five number summary is
Lowest value, Q1, Q2, Q3, Highest value
Looking at what we did above the five number summary for 1, 2, 3, 4, 6, 7, 12, 16, 19, 22, 31 is
1, 3, 7, 19, 31
And the five number summary for 1, 2, 3, 4, 6, 7, 12, 16, 19, 22, 31, 64 is
1, 3.5, 9.5, 20.5, 64
Outliers (Not Covered or Tested Fall 2016)
Sometimes a set of data contains a value that is suspiciously large or small, such a value may be an outlier. More Explanation
To check for outliers you find the interquartile range, which is IQR = Q3 ̶ Q1.
Then values bigger than Q3 + 1.5 IQR or less than Q1 ̶ 1.5 IQR are outliers
For the data 1, 2, 3, 4, 6, 7, 12, 16, 19, 22, 31, 64 given above
IQR = Q3 ̶ Q1 = 20.5 - 3.5 = 17
Then Q1 ̶ 1.5 IQR = 3.5 ̶ 1.5(17) = ̶ 22 and Q3 + 1.5 IQR == 20.5 +1.5(17) = 46
You conclude 64 is an outlier
Box Plots
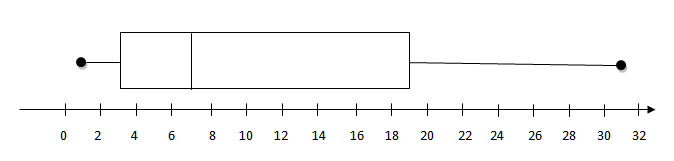
A box plot shows the five number summary in graphical form. You have dots above the smallest and highest values, lines above the quartiles and a box around the lines.
For 1, 2, 3, 4, 6, 7, 12, 16, 19, 22, 31 the box plot is:

Note that the box covers the range for the middle 50% of values