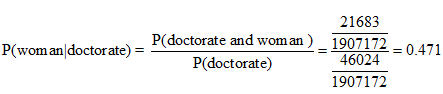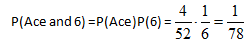
Multiplication Rules for Independent Events
Events A and B are independent if the occurrence of one does not affect the probability of the other occurring.
Example 1: Toss two coins.
Note: To figure probabilities it is best to think of things happening in succession. Think of this as tossing a first coin, then a second coin. You can even think of it as tossing one coin twice.
What is the probability of heads on both coins? You have independent events because what happens on one coin cannot affect probabilities for the second coin.
The sample space is HH, HT, TH, TT so P(2 heads) = 0.25
Another way to look at it is that you get heads half of the time on the first coin and then half of those times you will get heads on the second coin. So you get HH one half of one half of the time or one quarter of the time.
This illustrates the rule for independent events: P(A and B) = P(A)P(B)
Note: Providing events are independent regardless of the number of events you multiply probabilities
Example 2: Draw a card and roll a die. What is the probability you will get an ace and a 6?
The events are independent so
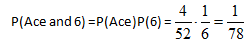
Example 3: In a recent election 53% of voters voted for candidate Jones. If three voters are selected at random
a. What is the probability all three voted for Jones?
The probability that any one voted for Jones is 0.53. So P(All three voted for Jones) = (0.53)(0.53)(0.53) = 0.149
Note: In this type of problem you may argue events are not independent because if you select a voter who voted for Jones there will be one fewer voters for Jones to select from for the second choice, making the selection less likely. However the 53% is likely not exactly correct and when large numbers are involved removing one voter will not make a significant difference. So in this type of problem regard events as independent.
b. What is the probability that none of them voted for Jones?
You look at the complement: P(did not vote for Jones) = 1 ̶ (voted for Jones) = 1 ̶ 0.53 = 0.47
P(None voted for Jones) = (0.47)(0.47)(0.47) = 0.104
c. What is the probability that at least one voted for Jones?
Note that "at least one" is the complement of "none": That is, if you not have at least one, you must have none.
P(At least one voted for Jones) = 1 ̶ 0.104 = 0.896
Note
Rules for Events That Are Dependent
Dependent means not independent
An example of dependent events is drawing two cards from a deck without replacement. As above treat it as drawing two cards in succession without replacing the first card.
Consider the events A: The first card is an ace and B: The second card is an ace.
If the first card is not an ace then you have 51 cards left, four of which are aces making P(second is an ace) = 4/51.
If the first card is an ace then you have 51 cards left, three of which are aces making P(second is an ace) = 3/51 = 1/17.
We have P(B|A), read as "P of B given A" for the probability that B occurs given that event A has already occurred. Above P(B|A) = 1/17.
Note: P(B|A) is called a conditional probability.
Note: For independent events P(B|A) = P(B).
Consider the event of drawing two cards. You would expect to gat an ace on the first card 1/13 of the time and then of those times getting an ace on the second card 1/17 of the time.
So you get two aces 1/17 of 1/13 of the time.
This is intended to illustrate the formula P(A and B) = P(A)P(B|A). So P(2 aces) = (1/13)(1/17) = 1/221
Example 1: A bag contains 6 red balls and 4 white balls. Two are drawn at random without replacement find:
a. P(both white)
For the first draw you have 10 balls, four of which are white making P(first white) = 4/10 = 2/5
You then have nine ball left, three of which are white making P(second white | first white) =3/9 = 1/3
Then, P(both white) = (2/5)(1/3) = 2/15
b. P(both red)
For the first draw you have 10 balls, six of which are red making P(first red) = 6/10 = 3/5
You then have nine ball left, five of which are red making P(second red | first red) =5/9
Then, P(both red) = (3/5)(5/9) =1/3
c. P(at least one white).
Treat it as a complement: 1 ̶ P(both red) = 1 ̶ 1/3 = 2/3.
Example 2: A box contains 12 cups, three of which are cracked. If you select three cups at random what is probability all are cracked?
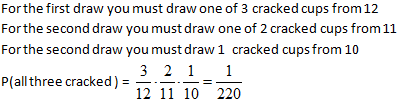
Calculating Conditional Probabilities
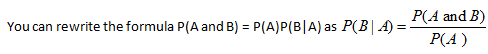
This is data from the last lesson
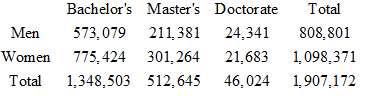
One degree is selected at random.
a. Find the probability that the degree is a doctorate given that it was awarded to a woman.
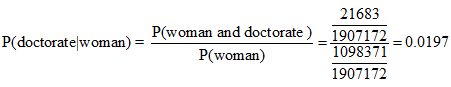
b. Find the probability that the degree was awarded to a woman, given it was a doctorate