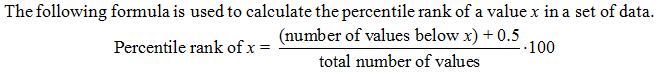
Measures of Position
Percentile Rank
The idea of a percentile is to measure how a score compares to other scores. For example if you are told that you scored at the 85th percentile on the SAT then it means you scored better than 85% of people who took the SAT. The percentile rank may not be exact: For example it may not possible to do better than, say, exactly 83 percent of 20 people. You should interpret 85% as "as close as you can get to 85%". Generally speaking percentiles are used for large data sets where some of the data will fall into each percentile. We show how to calculate them using small data sets where in reality the concept of a percentile is not very useful. This does not mean they are not useful in general.
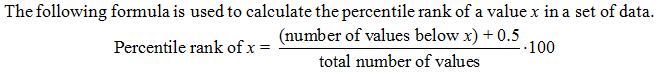
For example the data (which must be in order) is 2, 4, 5, 6, 6, 7, 11, 14, 23, 23, 25, 26, 29, 31. Find the percentile rank of 11.
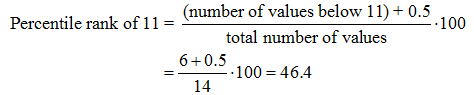
The percentile rank of 11 is 46. More Examples
How to Find the Value in a Set of Data Corresponding to a Percentile Rank
For example the data (which must be in order) is 2, 7, 15, 16, 26, 27, 31, 34, 37, 41, 44, 45, 48, 51, 53, 57. Find the 43rd percentile.
Let n be the number of data. Here n = 16. You find 43% of n = 0.43(16) = 6.88. If you do not get a whole number, as in this case, you round up to the next whole number, 7. Then the 7th value is the 43rd percentile. The 43rd percentile is 31.
Now find the 25th percentile: Find 25% of n = 0.25(16) = 4. When you get a whole number, in this case 4, you take the average of the fourth and fifth values = (16 + 26)/2 =21. The 25th percentile is 21 More Examples
z-scores
A z-score measures how far a value is from the mean in terms of standard deviations. You will see later that in many applications what matters is the z-score rather than the actual value.
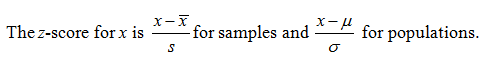
For example x = 24 find and s = 3.
(a) Find the z-score for x = 30.
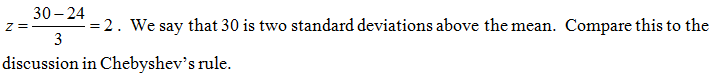
(b) Find the z-score for x = 19.5
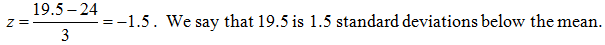
Finding x knowing the z-score
Often in problems when finding a value you first find the z-score, which you then convert to x.
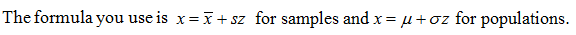
Algebra whiz's will recognize these are the z-score formulas solved for x.
For example µ = 24 find and σ = 3.
(a) Find the value of x corresponding to z-score z = 2.8
x = µ + σz = 24 + (2.8)3 = 32.4
(b) Find the value of x corresponding to z-score z = ̶ 1.3
x = µ + σz = 24 + ( ̶ 1.3)3 =20.1