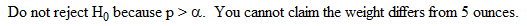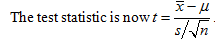
Testing a Population Mean When s is Unknown
In this lesson all the tests look exactly the same as they did when s was known. The difference is the test statistic is now t
and we use tcdf to calculate the p-value. Also we use the sample standard deviation s in place of s.
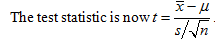
Example 1. A newspaper reports that the mean rental for apartments in Townsville is $650 per month. You look at 25 apartments and find the mean rental to be $700 with a standard deviation of $123. At a = 0.05 can you conclude that the mean rental is more than $650?
Note: This is a right tailed test because we are looking for the mean to be more than $650.
The set up: H0: m £ 650.
Ha: m > 650
Reject H0 if P < 0.05
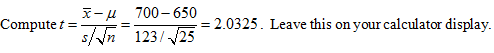
Note: As in any problem involving a t-distribution you have to take into account the degrees of freedom = d.f. = n - 1.
For a right-tailed test use tcdf(t, 10000, d.f.) = tcdf(ans, 10000, 24) = 0.0267.
Decision: Reject H0 because P < a. The mean rent is higher than $650.
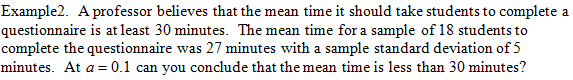
Note: This is a left tailed test because we are looking for the mean to be less than 30 minutes.
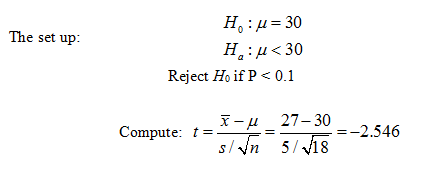
Note your book gives the null hypothesis as m ³ 30.
Since the test is left tailed we compute the area to the left of t.
P= tcdf(-10000,-2.546, 17) = 0.0104. (Recall d.f. = n - 1)
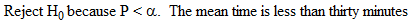
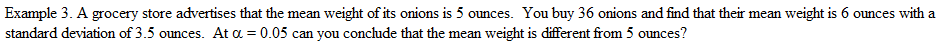
Note: This test is two
tailed because it asks if the mean differs from 5 ounces.
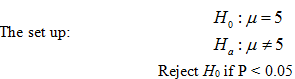
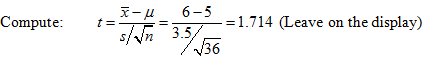
Note: Since t is in the right tail calculate the area to the right of t and double it because the test is two-tailed
Calculate P = 2tcdf(ans,10000, 35) = .0953. (Recall d.f. = n - 1)