Hypothesis Testing for m when s is known
Example 1: Consider the following problem: You are told that a population mean is 25 and the standard deviation is 5.
You want to determine if the mean is greater than 25. Suppose you take a sample of size 25 and find that the sample mean, X, is 28.
From this can you conclude with any degree of certainty that the mean is greater than 25?

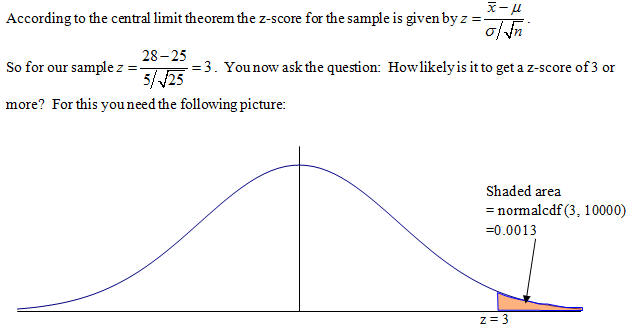
So the probability that z exceeds 3 is 0.0013, which is very unlikely and seems reasonable to conclude that the mean is greater than 25.
The probability that you make a wrong decision in saying that m > 25 is 0.0013. This probability is called the p-value, denoted P.
How Hypothesis Testing Works (Right-Tailed Test)
You have a null hypothesis denoted H0. In Example 1 you have H0: m = 25. See note below
You have an alternative hypothesis H1. The form of H1 depends on the problem.
In Example 1 you are checking if the mean is greater than 25, so you have Ha: m > 25.
You have a level of significance denoted a. usually a = 0.1, 0.05 or 0.01. You will always be given a in problems.
How Example 1 may be given as a question: A researcher claims that a population mean is 25 with a standard deviation 5. You suspect that the mean is greater than 25. You gather a sample and find the sample mean to be 28. Can you conclude that the mean is greater than 25 at the 0.01 significance level?
How to write the solution:
H0: m ≤ 25. A comment on How to Write H0
Ha: m > 25
Reject H0 if P < 0.01 Comment
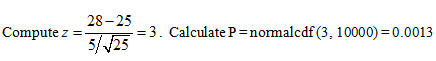
Reject H0, the mean is greater than 25. Another comment
Note: The test is right-tailed because we use an area in the right tail to compute P.
How Hypothesis Testing Works (Left-Tailed Test)
Example 2: You are told that a population mean is 25, with a standard deviation of 8. You claim the mean is less than 25. To test your claim you gather a sample of size 36 and find the sample mean is 24. Is your claim correct at the 0.05 significance level?
Note: In this problem the sample mean needs to be significantly less that 25 to support the claim. If it just a bit less than 25 it could be because of the usual variation in sample means.
How to write the solution:
H0: m ³ 25.
Ha: m < 25
Reject H0 if P < 0.05 Comment
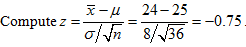
Since we are looking for a value less than 25, this time the picture for the p-value is:
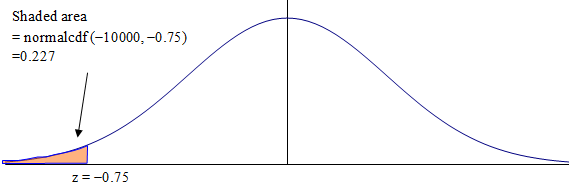
Calculate P = normalcdf (-10000, -.75) = 0.227
Do not reject H0. You cannot claim the mean is less than 25. Another comment
How Hypothesis Testing Works (Two-Tailed Test)
Example 3: You are told that a population mean is 32, with a standard deviation of 10. You claim the mean differs from 32. To test your claim you gather a sample of size 50 and find the sample mean is 28. Is your claim correct at the 0.1 significance level?
How to write the solution:
H0: m = 32
Ha: m ≠ 32
Reject H0 if P < 0.1 Comment
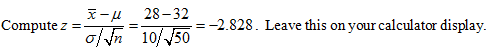
This time we are looking for a value that differs from 32. This will be the case if the mean is significantly less than 32 or significantly greater than 32.
This time the p-value is the probability of getting a value of z more extreme than the one we got. We use the following picture
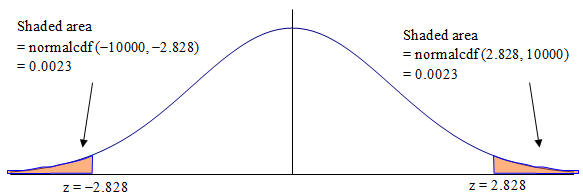
This time the p-value is double the area of one of the tails. Assuming you left z on the display it is P =2normalcdf( ̶ 10000, ans) = 0.0047.
Decision: Reject H0 because P < 0.1. The mean differs from 32
Example 4: You are told that a population mean is 32, with a standard deviation of 10. You claim the mean differs from 32. To test your claim you gather a sample of size 40 and find the sample mean is 33. Is your claim correct at the 0.05 significance level?
How to write the solution:
H0: m = 32
Ha m ≠ 32
Reject H0 if P < 0.05 Comment
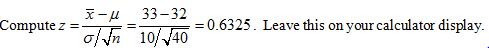
This time z is in the right tail, so find double the area right of z.
Assuming you left z on the display it is P =2normalcdf(ans, 10000) = 0.527
Decision: Do not reject H0 because P > 0.05. The mean does not differ from 32.