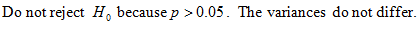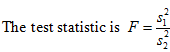
Testing if Two Standard Deviations or Variances Differ
The situation: You have two populations with variances s12 and s22. You want to test if one is greater than the other of if they differ. To do this you take two samples of sizes n1 and n2 and with variances s12 and s22. Always label the data so that s12 > s22 then all tests will either be right-tailed or two-tailed.
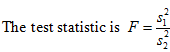
The degrees of freedom in the numerator is d.f.n. = n1 - 1.
The degrees of freedom in the denominator is d.f.d. = n2 - 1.
To calculate the area to the right of F use Fcdf(F, 10000, d.f.n, d.f.d)
Example 1: Gardner Joe wants to see if the weights of aubergines grown outside are more variable than weights of aubergines grown in controlled conditions under glass. He grows 25 aubergines outside and finds the variance in the weights, measured in ounces to be 7.6. He grows 30 aubergines under glass and finds the the variance to be 3.8. At a = 0.05 can he claim that the weights of aubergines grown outside are more variable than weights of aubergines grown under glass?
It can be helpful to summarize the data.
P = Fcdf(F, 10000, d.f.n, d.f.d) = Fcdf(2, 10000, 24, 29) = 0.038
Example 2: "Your onions are all the same size, the weights are not variable enough", complained Joe's wife. "What am I to do if the recipe calls for a large onion?" Joe thought to himself that she could use two. Instead he put on his false beard and dark glasses and headed for the supermarket where he purchased a bag of 20 onions. Everyone knew it was him because he did not change his signature gardening boots. Joe calculated the standard deviation of the weights of the store bought onions to be 40 grams and a sample of 17 of his own onions had a standard deviation of 35 grams. Is his wife's complaint justified? Use a = 0.1.
Be careful in this one: You are given the standard deviation, which you must square to get the variance. Do not forget to make
s12 > s22

P = Fcdf(F, 10000, d.f.n, d.f.d) = Fcdf(ans, 10000, 19, 16) = 0.297
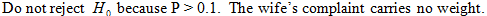
Example 3: A researcher took two samples of size 50 and found the variances to be 59.8 and 67.1. At the 0.05 significance level can he conclude the variances differ?
Remember to make s12 > s22

Since it is two-tailed double the area to the right of F. (You would have to do something different if s12< s22)
P =2 Fcdf(ans, 10000, 49, 49) = 0.6884