
Confidence Intervals for the Mean When σ is Unknown
In this section we assume that underlying populations are normal. Happily in nature populations tend to be normal
The procedure is very similar to the procedure when σ is known. You have to replace the z-distribution by a t-distribution.
The actual shape of a t-distribution depends on the sample size n. It looks similar to a z-distribution but is somewhat flatter and more spread out.
The curve is symmetric, the total area under the curve is 1 and in principle it extends for ever in both directions.

Notice that we use the sample standard deviation, rather than the population standard deviation.
Click the following link to get a t-table:
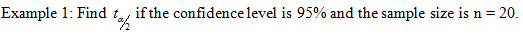
The t-table has three headings. Look under the heading for 95% confidence and across from d.f. = n -1 =19
In problems you will be required to calculate the mean and standard deviation; How to do it on the TI83+
Example 2: The following is the number of days it took to renovate a random sample of 10 run down houses:
25 75 38 41 27 32 36 53 49 54
Construct a 90% confidence interval for the mean time it takes to renovate a run down house.
From the TI83+ or TI84+ you find X = 43 and s = 15.1291

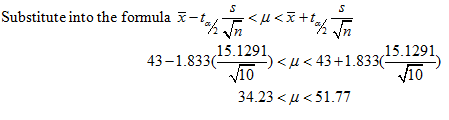
The 90% confidence interval is 34 days to 52 days.