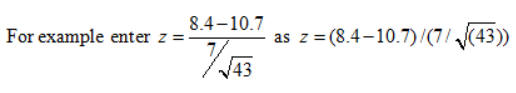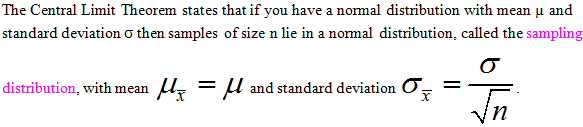
The Central Limit Theorem
Suppose you have a distribution with mean m and standard deviation σ. Say m = 12 and σ = 5. If you select one value X at random from the population you know how to answer questions like:
What is P(X >14)? or What is P(11 < X < 14.3)?
Now suppose you take a sample of size n from the population and calculate its mean X. Can you answer questions like: What is P(X > 14)?
The answer is, 'Yes you can' if you know the central limit theorem.
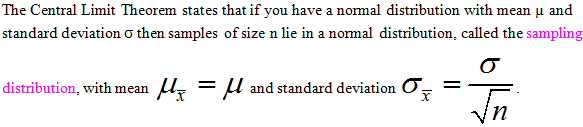
(I had to enlarge the symbols to make the bar over the x visible!)
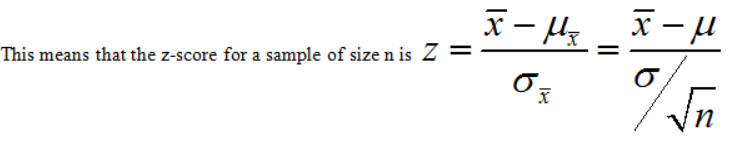
Example 1: Suppose you have a normal distribution with mean m = 12 and standard deviation σ = 5. If you take a sample of size 16 from the population what is P(X > 14)?
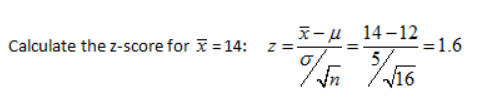
Then P(X > 14) = P(z > 1.6) = normalcdf(1.6, 10000) = 0.0548
Example 2: The mean consumption of ice cream by high school juniors at a party is 10.7 ounces with a standard deviation of 3 ounces.
a. What is the probability that a randomly selected junior consumes less than 8 ounces?
b. What is the probability that a sample of 36 juniors has a mean consumption less than 8 ounces?
c. What is the probability that a sample of 36 juniors has a mean consumption between 10.3 ounces and 11.1 ounces?
d. Why might this type of information be useful?

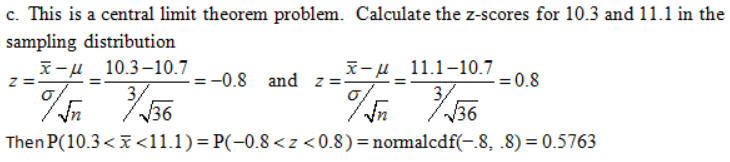
d. If you were supplying ice cream to 36 juniors it is extremely unlikely that 8 ounces per person would be enough. At least you would be sure to have none left!
Note: If the distribution for the population is not normal then the sampling distribution will in general not be normal. A second part of the central limit theorem is that regardless of the population's distribution the sampling distribution will be close enough to normal for practical purposes if n is big enough. You can usually assume the sampling distribution is normal if n is at least 30
Note: Students commit too many calculator errors in these problems. If you want to evaluate a complicated fraction in one step put the numerator and denominator in parentheses.