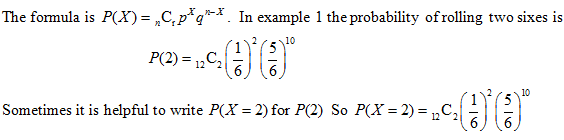
Binomial Distributions
Example 1: An example where you get a binomial distribution is to roll a die 12 times and count the number of sixes
You perform an identical experiment n times. Each performance of the experiment is a trial. On each trial you have success or failure and the probability of success, p, is the same on each trial.
In Example 1 there are 12 trials, namely rolling a die 12 times. On each trial success is rolling 6 and p = 1/6.
We use q for the probability of failure, which is not rolling a 6 in Example 1. It is always true q = 1 ̶ p, so in Example 1 q = 5/6.
We use P(X) for the probability of getting X successes in the n trials.
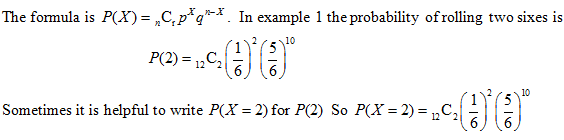
We evaluate P(X = k) on the TI83+ using binompdf(n, p, k).
There is a distribution key which above VARS, which brings up a list of distributions, most of which we will get to.
To calculate P(X = 2) enter binompdf(12, 1/6, 2) = 0.2961
Example 2: Toss a coin 20 times. What is the probability of getting 9 tails?
Here n = 20, p = 1/2 and X = 9. It is binompdf(20, 1/2, 9) or binompdf(20, .5, 9) = 0.1602
Example 3: The chance of rain is 30% every day next week. What is the probability it will rain of 4 of the seven days?
Here n = 7, p = 0.3 and X = 4. It is binompdf(7, .3, 4) = 0.0972
Cumulative probabilities
Often we are interested in problems of the type: If you toss 20 coins what is the probability you get at most 12 heads?
On the TI83+ this is calculated using P(X ≤ 12) =binomcdf(20, .5, 12)
BE CAREFUL. IF YOU HAVE SOMETHING OTHER THAN P(X ≤ k) A MODIFICATION IS NEEDED!
Example 4: If you toss 20 coins what is the probability you get fewer than12 heads?
"Fewer than 12" is the same as "at most 11". It is calculated using P(X ≤ 11) =binomcdf(20, .5, 11) = 0.7483
Example 5: If you roll 15 identical dice what is the probability you get more than three ones?
You treat this as a complement. "More than three" is the complement of "at most three"
It is calculated using 1 ̶ P(X ≤ 3) = 1 ̶ binomcdf(15, 1/6, 3) = 0.2315
Example 6: If you roll 15 identical dice what is the probability you get at least three ones?
"At least three" is the complement of "at most two"
It is calculated using 1 ̶ P(X ≤ 2) = 1 ̶ binomcdf(15, 1/6, 2) = 0.4678
Mean Variance and Standard Deviation
If you rolled 30 dice repeatedly on average how many sixes would you expect to get?
It is reasonable to expect the average to be five since you get a six one sixth of the time.
You get this from the formula E(X) = m = np
It is beyond the scope of this course to justify it, but the formula for variance is s2 = npq
Standard deviation is the square root of the variance.
Example 6: Roll a die 180 times then:
m = np =180(1/6) = 20
s2 = npq = 180(1/6)(5/6) = 25
s = 5
Note: It is a fact that for fairly large values of n binomial distributions follow the empirical rule.
Recall about 68% of values are within one standard deviation of the mean and about 95% of values are within two standard deviations of the mean.
If you roll a die 180 times (or 180 dice once) you can expect the number of sixes to be between 15 and 25 about 68% of the time
and to be between 10 and 30 about 95% of the time.